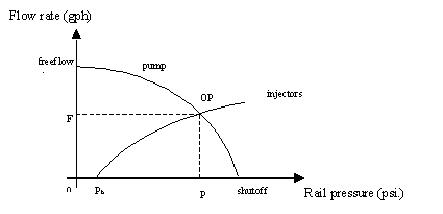
The operating point (OP) results from a supply vs demand relationship. The pump is the supply and the injectors are the demand. If you were to plot the pump flow versus pressure and the injector flow characteristics on the same graph, you will find they intersect at some point. You will find that the fuel system will operate somewhere on the injector curve. If the desired OP is inside (to the left of) the supply curve, then the pump will have sufficient headroom (reserve capacity) and pressure will be maintained by the regulator. If the desired OP is outside the supply, then the OP will be the intersection. Put simply, demand cannot exceed the supply.

The fuel pump used in the Turbo 3.8 is a constant-power type with flow determined by regulated pressure. From the rocket equation (check the old physics book) flow through the injector is proportional to the square root of the pressure differential across it, i.e. doubling the pressure results in 1.41 times the flow. The pump and injector flow versus pressure curves are plotted below (all 6 injectors added up, in gph). The pump graph can be obtained from manufacturer’s or test data. The injector graph can be constructed from just one point (F1 pph @ P1 psi) and the rest from the square-root relation: .

Note: The new flow (F2) is calculated using delta-P but plotted by adding Pb to get total pressure.

This plot was done using some assumptions: WOT, 100% duty cycle, constant boost (Pb), const. voltage and fixed pressure set-point (delta-P). Assume you want the absolute max flow from this combination. The intersection point (OP) has a pressure P and flowrate F associated with it. This is a stable operating point. It’s stable in that a slight decrease in pressure results in the injector flow decreasing, but pump flow increasing. So flow wants to migrate back to the operating point. The same holds true for a slight increase in pressure: The pump flow decreases but injector flow increases, moving back to the original OP.

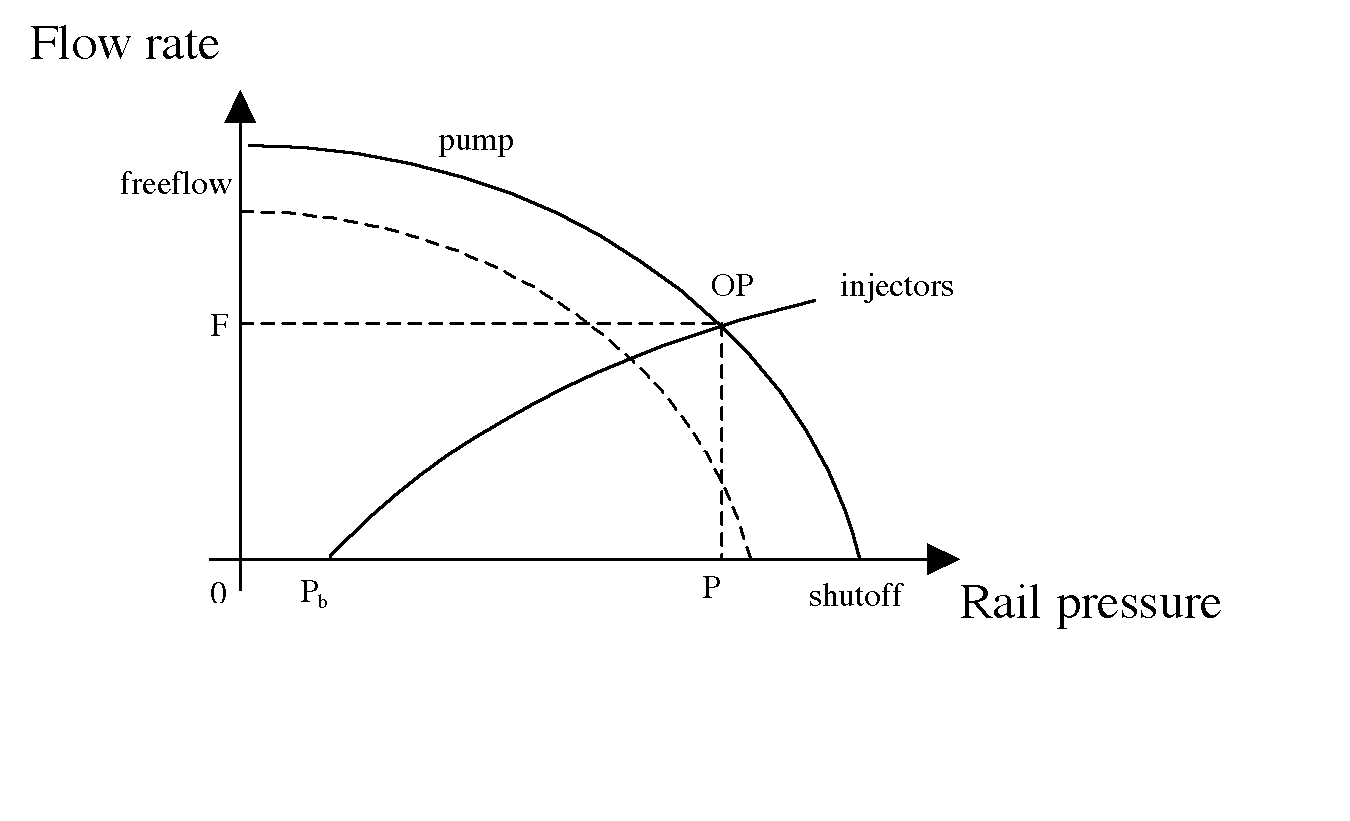
What happens with larger injectors and the same pump? A larger injector (with the same pump) moves the OP up/left (higher flow with lower pressure). It’s easy to see that with larger injectors, where you had sufficient pump capacity before, you may now need a larger pump. Below, the lager injectors are plotted with the solid line and the previous injectors are dashed. A smaller injector moves the OP down/right (lower flow with higher pressure).

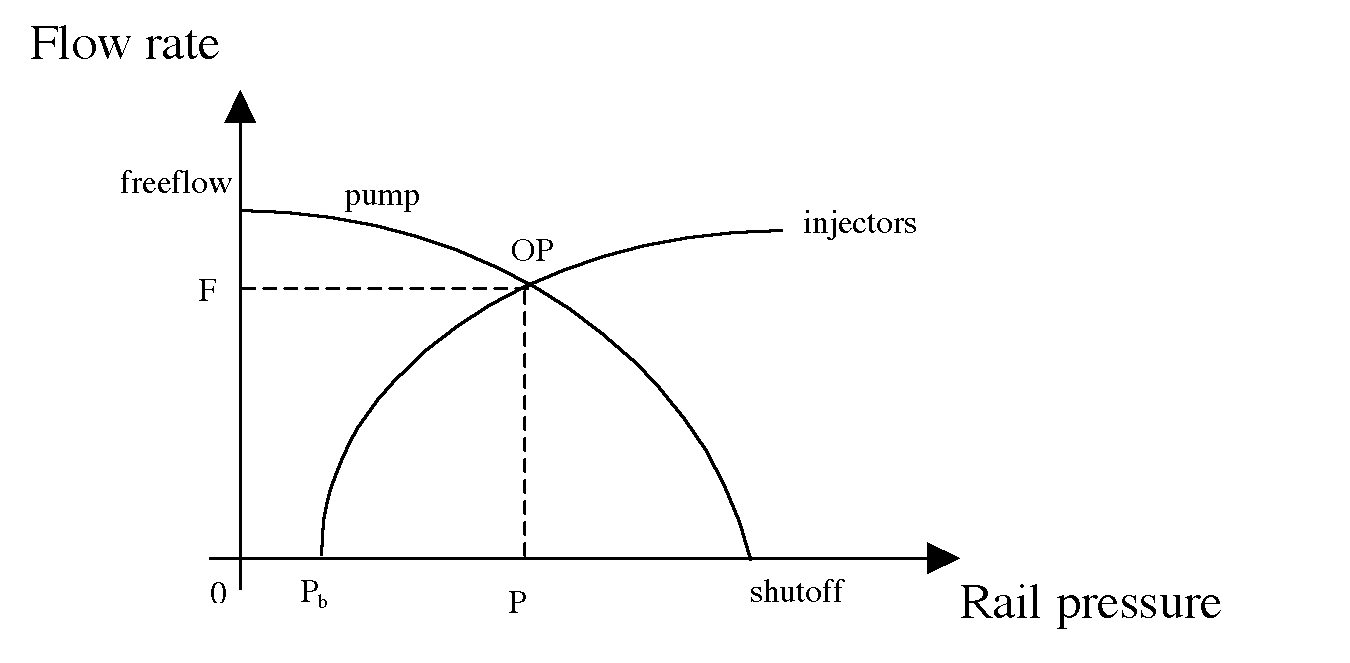
A larger pump (with the same injectors) moves the OP up/right (higher flow with higher pressure). Below, the larger pump is plotted with the solid line. It’s easy to see why a larger pump gives you more headroom (capacity) . A smaller pump moves the OP down/left.

Well, now for a numerical example. Assume you have the green stripe injectors (30 pph @ 43.5 psi) with a GSS242 pump, 20 psi boost, WOT, 100% duty cycle. Plotting the injector data on the pump plot (at 12v) off the web, I get the OP to be 32 gph at 70 psi. This corresponds to a delta-P of 50 psi. So the max flow you could hope to get from this particular combination is 32 gph, at 50 psi with the vacuum hose off. This turns out to be about 385 hp — assuming a BSFC of 0.5. These numbers and this method are not exact but should you pretty close. Hope this helps someone.